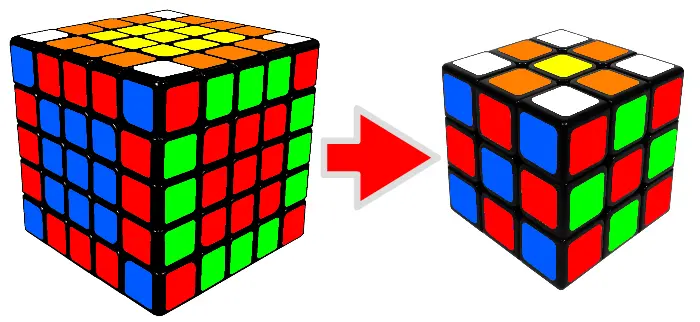
Jak ułożyć Kostkę Rubika 5×5?

Kostkę Rubika 5×5 można ułożyć wykorzystując etapy układania kostki 3×3. Najpierw jednak trzeba ułożyć środki ścianek, a następnie sparować krawędzie. Po tych dwóch wstępnych etapach można przejść do etapów znanych z kostki 3×3. Na tej stronie dowiesz się jak ułożyć kostkę Rubika 5×5 krok po kroku.

Spis treści

• Oznaczenia kostki
• ETAP 1 – Środki
• ETAP 2 – Krawędzie
• Błąd parzystości
• Podwójny błąd parzystości
• ETAP 3 – Tak samo jak 3×3
• Inne instrukcje

Oznaczenia ścianek

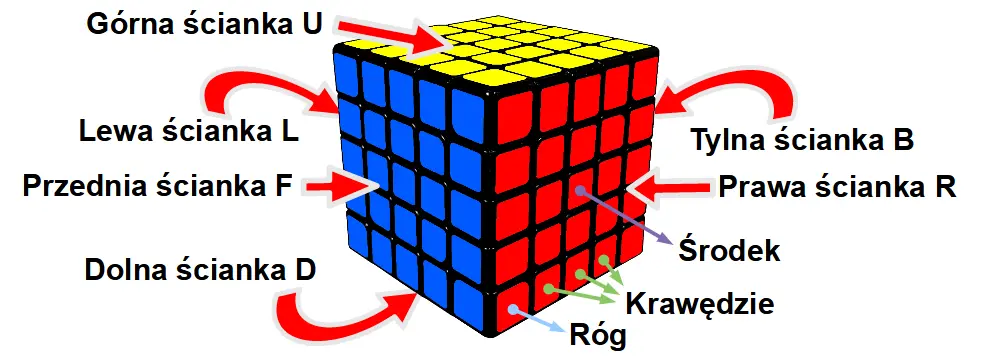
Środek – to klocek o jednym kolorze. Na każdej ściance jest po 9 takich klocków. Tak jak w kostce 3×3, jeden wewnętrzny środkowy klocek nie zmienia swojego położenia względem środków na innych ściankach

Róg – to klocek o 3 kolorach. Na każdej ściance są po 4 rogi

Krawędź – to klocek o dwóch kolorach. W tej kostce pomiędzy dwoma rogami są po 3 klocki będące krawędziami. Na każdej ściance jest w sumie po 12 klocków – krawędzi

Oznaczenia ruchów

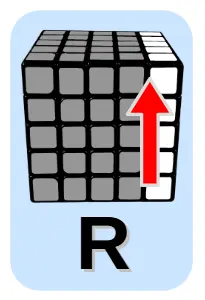
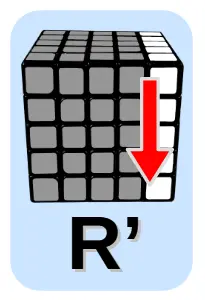
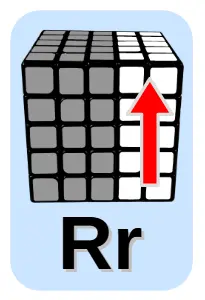
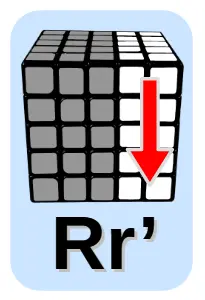
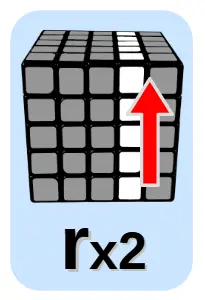
Ruchy oznaczone są literami:

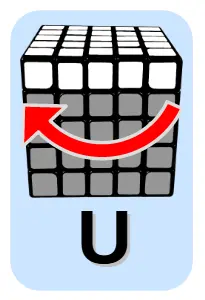
• U – ruch górną ścianką (ang. Up)
• D – ruch dolną ścianką (ang. Down)
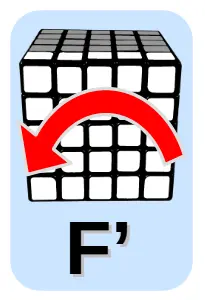
• F – ruch przednią ścianką (ang. Front)
• R – ruch prawą ścianką (ang. Right)
• L – ruch lewą ścianką (ang. Left)

• Duże litery: U, D, F, R, L – oznaczają ruch zewnętrzną ścianką
• Małe litery: u, d, f, r, l – oznaczają ruch środkową ścianką
• Duża litera + mała litera: Uu, Dd, Ff, Rr, Ll – oznaczają ruch obiema ściankami jednocześnie
• x2 – oznacza podwójny ruch, czyli obrót o 180 stopni – 1/2 pełnego obrotu

Ruchy wykonuj trzymając kostkę frontem „F” skierowanym do siebie.

Każdy ruch to obrót ścianki o 90 stopni, czyli 1/4 pełnego obrotu. Oznaczenia ruchów:

• bez apostrofu – to obrót ścianki zgodnie z ruchem wskazówek zegara
• z apostrofem – przeciwnie do ruchu wskazówek zegara

ETAP 1 – Środki

Pierwszy etap to ułożenie środków – czyli 9 środkowych klocków na każdej ściance.

Poniżej przedstawiono kolejno proces łączenia środków. Najpierw łączymy ze sobą dwa klocki (1+1) tego samego koloru, następnie do nich kolejną parę (2+2), następnie do nich dołączamy kolejne 2 środki (4+2), a na koniec ostatnie 3 środki (6+3).

Warto najpierw ułożyć dwie pierwsze ścianki naprzeciw siebie – ułatwi to późniejsze układanie pozostałych czterech ścianek.

Pod koniec tego etapu mogą przydać się dwa dodatkowe algorytmy na wymianę 1 klocka pomiędzy ściankami w zależności od jego położenia.

Gdy klocki, które chcesz połączyć nie znajdują się na sąsiadujących ściankach tylko na przeciwległych, to wykonaj ruchy „Rr” dwukrotnie obracając tym samym obie prawe ścianki o 180°.

Krok 1 – Połączenie środków 1+1

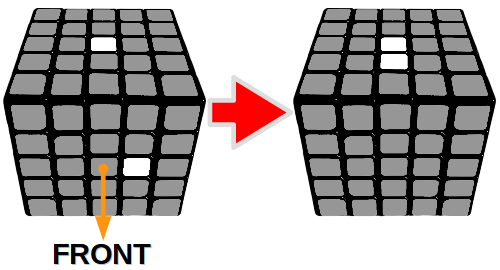
Krok 2 – Połączenie środków 2+2

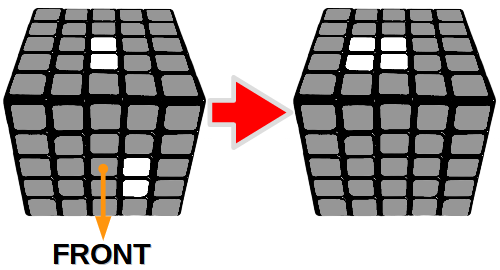
Krok 3 – Połączenie środków 4+2

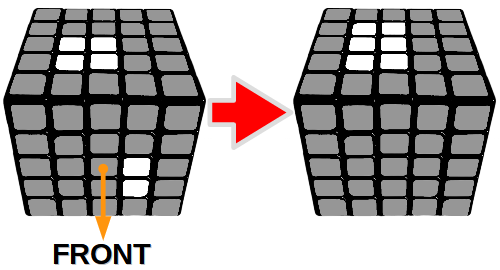
Algorytm do kroków 1, 2, 3

Krok 4 – Połączenie środków 6+3

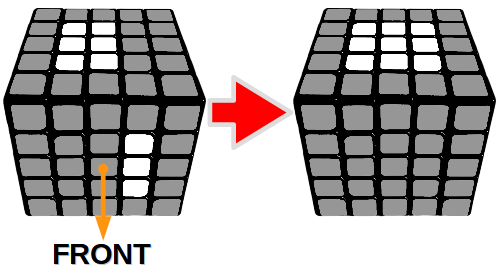
Dodatkowa sytuacja 1

Zamiana klocka z przedniej ścianki z klockiem na ściance górnej

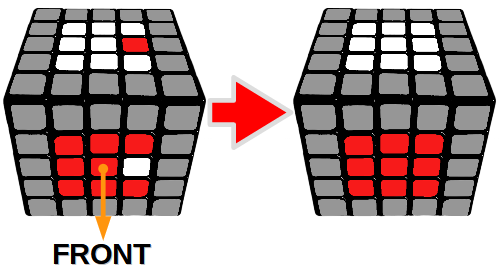
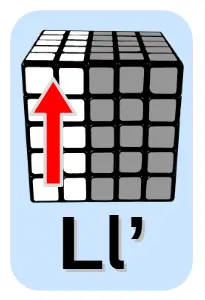
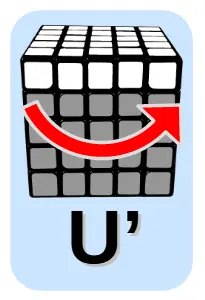
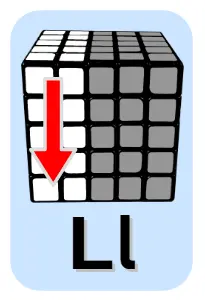
Dodatkowa sytuacja 2

Zamiana klocka z przedniej ścianki z klockiem na ściance górnej

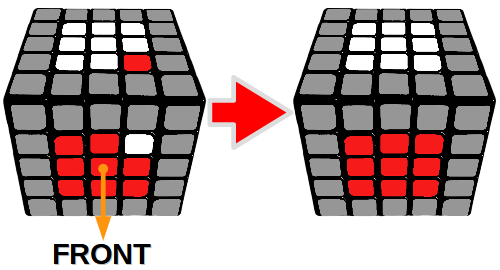
Gdy ułożysz już wszystkie środki, przejdź dalej do ETAPU 2.

ETAP 2 – Krawędzie

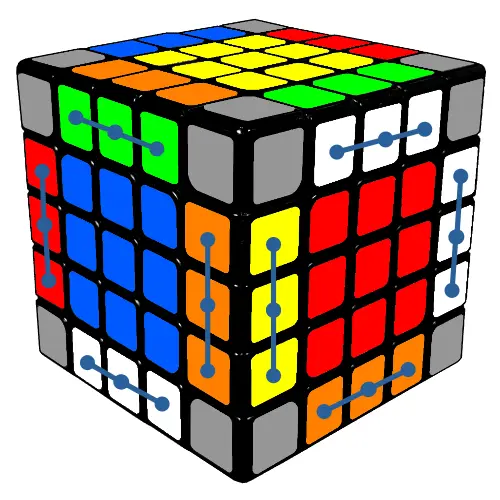
Drugi etap to ułożenie wszystkich 12 krawędzi w taki sposób, aby 3 klocki w obrębie jednej krawędzi były takie same.

Dwa pierwsze poniższe algorytmy są podstawowe. Dzięki nim połączysz większość krawędzi. Następne algorytmy służą głównie do łączenia dwóch ostatnich krawędzi.

Algorytm podstawowy 1

Połączenie prawego dolnego klocka krawędzi ze środkowym górnym klockiem krawędzi – psuje krawędź lewą „XX”

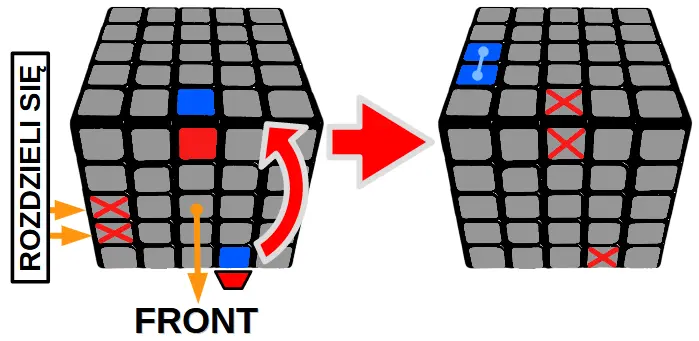
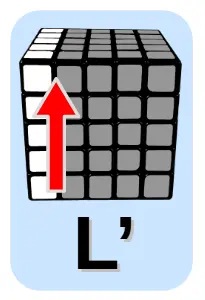
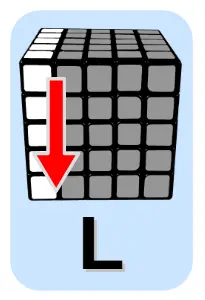
Algorytm podstawowy 2

Połączenie lewego dolnego klocka krawędzi ze środkowym górnym klockiem krawędzi – psuje krawędź prawą „XX”

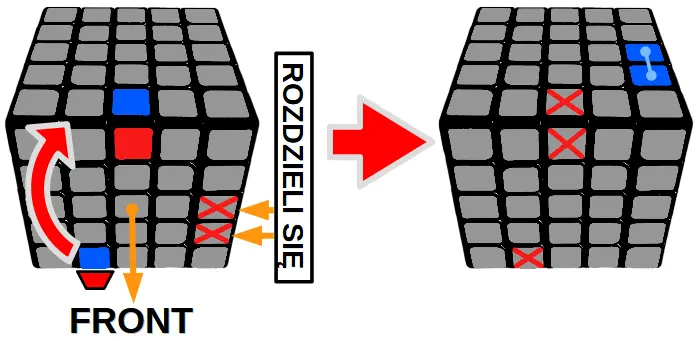
Algorytm 3

Zamiana środkowego klocka pomiędzy dwoma górnymi krawędziami.
Wersja 1: jedna z krawędzi ma 3 takie same kolory na górnej warstwie (zielony)

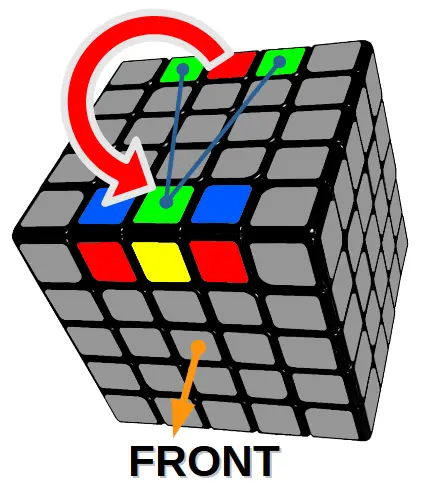
Algorytm 4

Zamiana środkowego klocka pomiędzy dwoma górnymi krawędziami.
Wersja 2: obie krawędzie mają po 2 kolory takie same w górnej warstwie

Algorytm 5

Zamiana środkowego klocka pomiędzy dwoma górnymi krawędziami.
Wersja 3: obie krawędzie mają po 3 kolory takie same w górnej warstwie

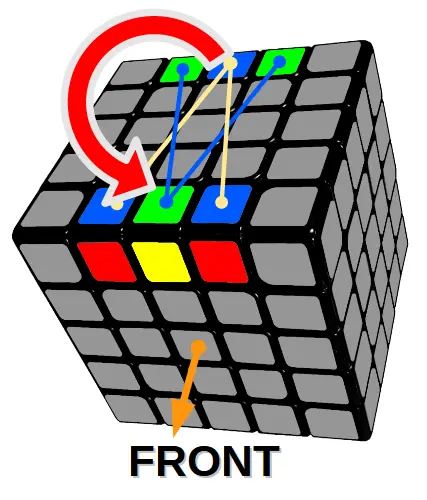
Algorytm 6

Zamiana klocków po skosie pomiędzy dwoma górnymi krawędziami (prawy klocek)

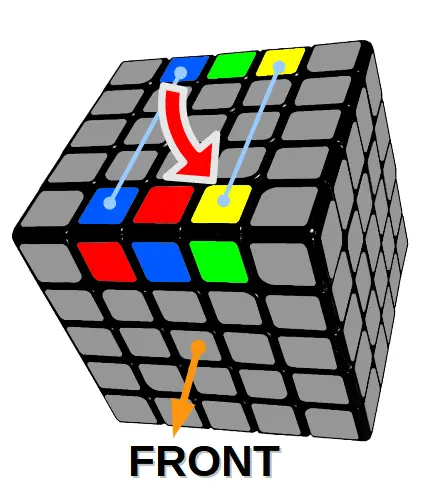
Algorytm 7

Zamiana klocków po skosie pomiędzy dwoma górnymi krawędziami (lewy klocek)

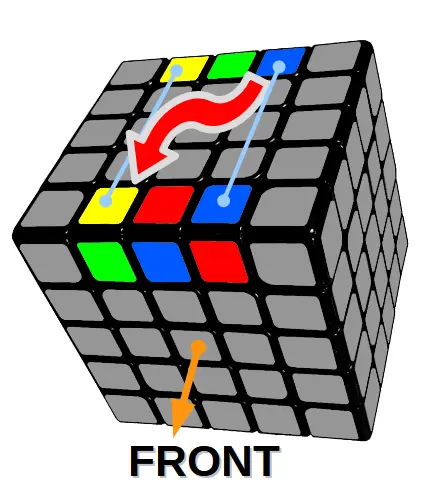
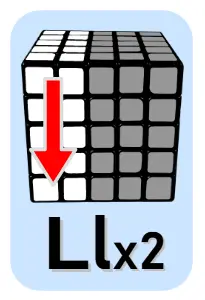
Algorytm 8

Zamiana klocków po skosie pomiędzy dwoma górnymi krawędziami (prawy klocek)

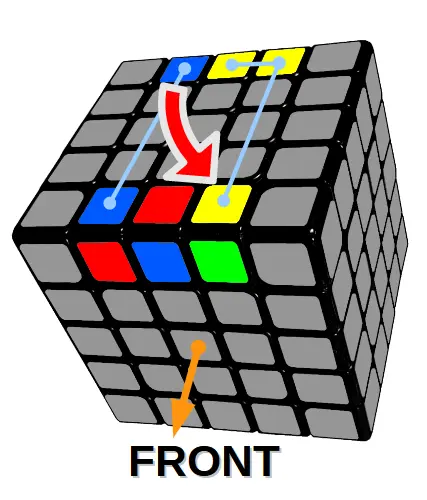
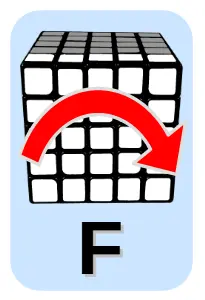
Algorytm 9

Zamiana klocków po skosie pomiędzy dwoma górnymi krawędziami (lewy klocek)

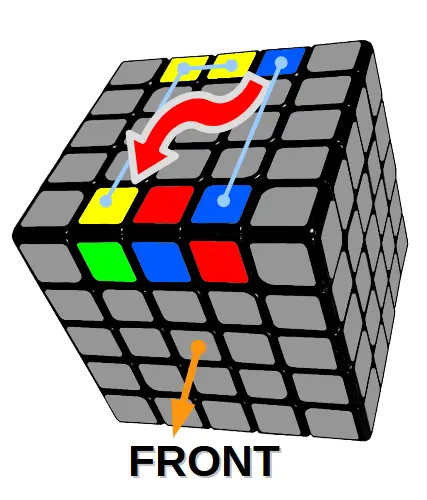
Algorytm 10

Zamiana prawego klocka pomiędzy dwoma górnymi krawędziami

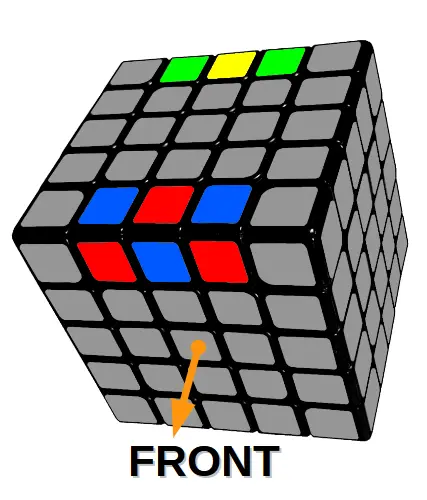
Błąd parzystości

Błąd parzystości na jednej krawędzi

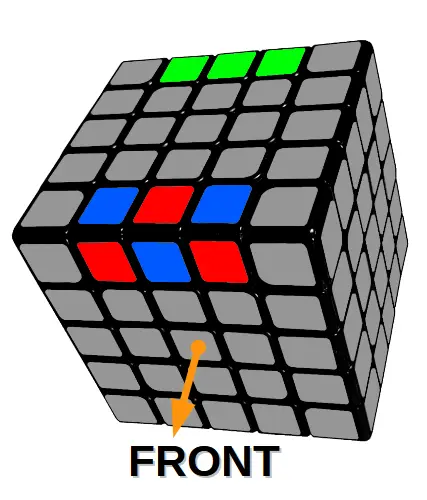
Podwójny błąd parzystości

Błąd parzystości na obu krawędziach

Gdy ułożysz już wszystkie krawędzie, przejdź dalej do ETAPU 3.

ETAP 3 – Tak samo jak 3×3

Trzeci etap to ułożenie kostki do końca w taki sam sposób, jak układa się kostkę 3×3.

Sposób Układania

Podczas układania wg instrukcji kostki 3×3, obracaj tylko zewnętrznymi ściankami kostki, nie psując środków.

Gratulacje. Już wiesz jak ułożyć kostkę Rubika 5×5!

Instrukcje układania kostek

Kostka 2×2

Kostka 3×3
LBL (Łatwa)

Kostka 3×3
CFOP (Trudna)

Kostka 4×4

Kostka 5×5

Kostka
Piramida

Kostka Skewb

Kostka
Megaminx 2×2

Kostka
Megaminx 3×3

Nasz sklep z kostkami